Task 1: Modeling

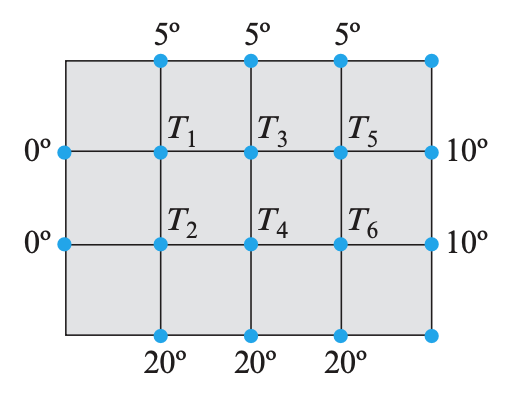
The figure below shows a metal plate whose edges are held at the temperatures shown. It follows from thermodynamic principles that the temperature at each of the six interior nodes will eventually stabilize at a value that is approximately the average of the temperatures at the four neighboring nodes. These are called the steady-state temperatures at the nodes.

Find a linear system whose solution gives the steady-state temperatures at the nodes, and use scipy to solve that system.

Task 2

Show that if $A$ is a square matrix that can be reduced to a row echelon form $U$ by Gaussian elimination without row interchanges, then $A$ can be factored as $A = LU$, where $L$ is a lower triangular matrix.

Show that the LU decomposition can be rewritten as

\[A=LDU\]

where now both the lower triangular factor and the upper triangular factor have 1’s on the main diagonal.

Task 3

Propose an efficient method for solving $Ax=b$ and $A^T\tilde{x}=\tilde{b}$.

Task 4

Find the LU decomposition of the matrix

\[A=\begin{bmatrix} 3 &−6 &−3 \\ 2 &0 &6 \\ −4 &7 &4 \end{bmatrix}.\]

Using the decomposition:

• solve the system of linear equations: $Ax=b$ when $b=[-3, -22, 3]$
• find the inverse of $A$.

Task 5

Software libraries vary in how they handle LU-decompositions. For example, many libraries perform row interchanges to reduce roundoff error and hence produce PLU-decompositions, even when asked for LU-decompositions. Find out which function(s) performs the LU-decomposition in Python Scipy and see what happens when you use scipy to find an LU-decomposition of the matrix from the previous task. (Hint: compare scipy.linalg.lu, scipy.linalg.lu_factor, scipy.linalg.lu_solve, scipy.sparse.linalg.splu). Update your implementation of Task 1 such that it does not need to compute any matrix inversion.

Task 6: Linear Programming by Affine Scaling

Implement in python the affine-scaling method and solve the following problem:

\[\begin{array}{rl} \max\;& z=x_1+2x_2\\ &x_1+x_2\leq 8\\ &x_1\geq 0,x_2\geq 0 \end{array}\]

It is the same problem as seen in the slides. But now solve it assuming the starting solution is $[x_1, x_2]=[1, 3]$. The optimal solution is $[0,8]$.

You can then solve also the following problem:

\[\begin{array}{rl} \text{maximize} \;\;&2x_1 + 3x_2 + 2x_3 \\ \text{subject to} \; \; &x_1 + x_2 +2x_3 = 3\\ &x_1,x_2,x_3 \geq 0. \end{array}\]

using as starting solution $[x_1, x_2, x_3]=[1, 3/2, 1/4]$.

How should the algorithm change if the problem was a minimization problem?

Task 7: Linear Programming for Project Selection

Model in linear programming terms the following problem: Given a set of projects to invest on, each with a cost and an expected profit, determine which to include in a collection so that the total cost is less than or equal to a given budget and the total expected profit is as large as possible. Reason about the nature of the variables, continuous or discrete.

Solve the instance of the problem given in the python code below in two ways:

• with scipy.optimization.linprog from the latest versions of scipy,

• with your implementation of the Affine Scaling method seen in the lecture.

The previous solution methods will only solve the continuous variables case. It is anyway a good exercise to solve the problem with continuous variables and then try to derive an integer solution from the fractional one. How would you do?

import numpy as np

num_items=100
capacity=997
profit = np.array([585, 194, 426, 606, 348, 516, 521, 1092, 422, 749, 895, 337, 143, 557, 945, 915, 1055, 546, 352, 522, 109, 891, 1001, 459, 222, 767, 194, 698, 838, 107, 674, 644, 815, 434, 982, 866, 467, 1094, 1084, 993, 399, 733, 533, 231, 782, 528, 172, 800, 974, 717, 238, 974, 956, 820, 245, 519, 1095, 894, 629, 296, 299, 1097, 377, 216, 197, 1008, 819, 639, 342, 807, 207, 669, 222, 637, 170, 1031, 198, 826, 700, 587, 745, 872, 367, 613, 1072, 181, 995, 1043, 313, 158, 848, 403, 587, 864, 1023, 636, 129, 824, 774, 889])
cost = np.array([485, 94, 326, 506, 248, 416, 421, 992, 322, 649, 795, 237, 43, 457, 845, 815, 955, 446, 252, 422, 9, 791, 901, 359, 122, 667, 94, 598, 738, 7, 574, 544, 715, 334, 882, 766, 367, 994, 984, 893, 299, 633, 433, 131, 682, 428, 72, 700, 874, 617, 138, 874, 856, 720, 145, 419, 995, 794, 529, 196, 199, 997, 277, 116, 97, 908, 719, 539, 242, 707, 107, 569, 122, 537, 70, 931, 98, 726, 600, 487, 645, 772, 267, 513, 972, 81, 895, 943, 213, 58, 748, 303, 487, 764, 923, 536, 29, 724, 674, 789])

Task 8

Consider the following LP problem:

\[\begin{align*} \max \quad &5x_1 + 4x_2 + 3x_3 \\ \text{s.t.} \quad &2x_1 + 3x_2 + x_3 \leq 5 \\ &4x_1 + x_2 + 2x_3 \leq 11 \\ &3x_1 + 4x_2 + 2x_3 \leq 8 \\ &x_1,x_2,x_3 \geq 0 \end{align*}\]

and an initial solution $\vec x = \begin{bmatrix} 0.5, 1, 0.5\end{bmatrix}$. Solve the problem with the Affine Scaling method.

Task 9

Show that if $A$ is a real-valued symmetric (hence square) positive definite matrix, then $A$ can be factored as $A = LL^T$, where $L$ is a lower triangular matrix and $L$ is unique.

Show that the Cholseky decomposition can be rewritten as

\[A=LDL^T\]

where now the diagonal elements of $L$ are required to be 1 and $D$ is a diagonal matrix.

Task 10

Propose an efficient method for solving $Ax=b$ where $A$ is a real-valued symmetric positive definite matrix.

Task 11

Test whether the following martix is positive definite:

\[A=\begin{bmatrix} 3 &2 &−4 \\ 2 &0 &7 \\ −4 &7 &4 \end{bmatrix}.\]

If it is not, generate a positive definite matrix from it and find its $LL^T$ decomposition. Using the decomposition:

• solve the system of linear equations: $Ax=b$ when $b=[-3, -22, 3]$
• find the inverse of $A$.

Task 12

Find out which function(s) performs the Cholseky decomposition in Python Scipy and see what happens when you use scipy to find a Cholesky decomposition of the matrix from the previous task. (Hint: compare scipy.linalg.cholesky, scipy.linalg.cho_factor, scipy.linalg.cho_solve.)

Task 13

Update the Affine Scaling algorithm above to use the Cholesky decomposition and resolve the LP problems above.