DM587 (E24) - Scientific Programming

Task 1

Show that for an $n\times n$ matrix $E$ whose columns are the vectors of an orthonormal basis $E^{-1}=E^T$.

Solution:

See solution in Appendix 1 of the tutorial.

Task 2

Show that for any $m\times n$ matrix $A$, $AA^T$ is a symmetric matrix of size $m\times m$ and $A^TA$ is a symmetric matrix of size $n\times n$.

Solution:

See solution in Appendix 2 of the tutorial.

Task 3

Show that a real matrix is symmetric if and only if it is orthogonally diagonalizable.

Solution:

See solution in Appendix 3 of the tutorial.

Task 4 - PCA Visually

Consider 100 students with Physics and Statistics grades shown in the two diagrams below.

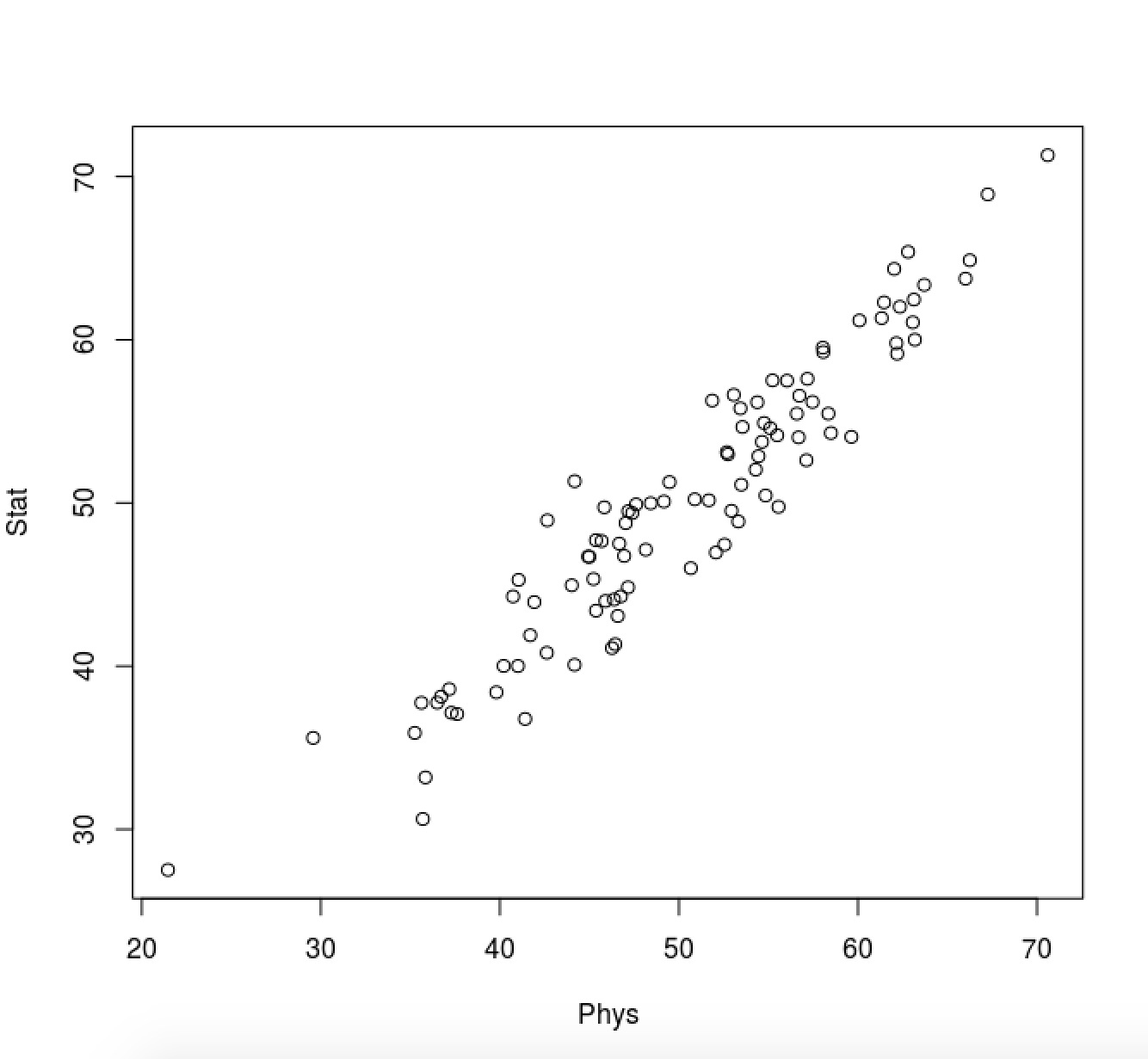
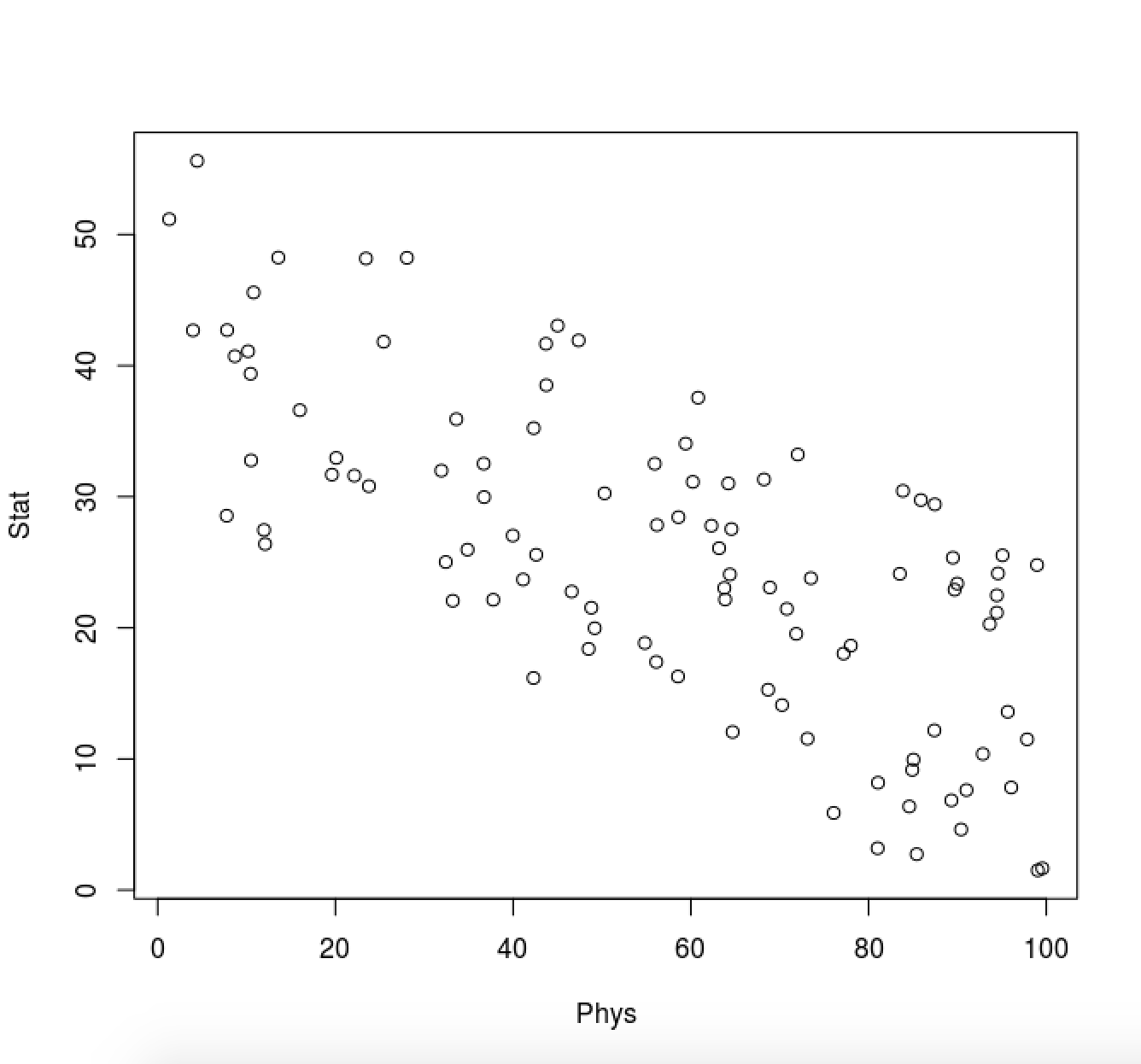
points1 points2

For each diagram:

  1. Which is the direction (as a vector) along which the data varies the most?

  2. What is (roughly) the point representing the mean value of the statistics/mathematics degree?

Solution:

The figures below are annotated with

  1. the direction the data varies the most

  2. the point representing the mean value (roughly)

points1 points2

Task 5 - Covariance Matrix

Assume the following grades:

    Student   Math   English   Art
  --------- ------ --------- -----
          1     90        60    90
          2     90        90    30
          3     60        60    60
          4     60        60    90
          5     30        30    30

  1. Define a matrix $X’$ where the rows represent samples (students), and the columns represent features (the different tests).

  2. Perform mean centering: subtract each data value from its variable’s measured mean so that its empirical mean (average) is zero, call the resulting matrix $X$.

  3. Without computing, what do you expect the covariance between a) Math and English and b) English and Art to be? Postive or negative?

  4. Ignoring Bessel’s correction, which formula must be used to compute the covariance matrix?

  5. Compute the variance of each test grades and the covariance between the test grades.

  6. Determine the covariance matrix a) with Bessel’s correction, b) without Bessel’s correction.

Solution:

(1.) The matrix is

\[\begin{align*} X' = \begin{bmatrix} 90 & 60 & 90 \\ 90 & 90 & 30 \\ 60 & 60 & 60 \\ 60 & 60 & 90 \\ 30 & 30 & 30 \\ \end{bmatrix} \end{align*}\]

The i’th row represents student $i$ (1-indexed), ie. the feature values for that student. The first column holds math grades, the second english grades, and the third art grades.

(2.) The averages for the features are

  • Math: $\frac{1}{5}\cdot (90+90+60+60+30) = 66 $

  • English: $\frac{1}{5}\cdot (90+90+60+60+30) = 60 $

  • Art: $\frac{1}{5}\cdot (90+90+60+60+30) = 60 $

For each entry we subtract the corresponding mean for the column. We obtain

\[\begin{align*} X = \begin{bmatrix} 66-90 & 60-60 & 60-90 \\ 66-90 & 60-90 & 60-30 \\ 66-60 & 60-60 & 60-60 \\ 66-60 & 60-60 & 60-90 \\ 66-30 & 60-30 & 60-30 \end{bmatrix} = \begin{bmatrix} -24 & 0 & -30 \\ -24 & -30 & 30 \\ 6 & 0 & 0 \\ 6 & 0 & -30 \\ 36 & 30 & 30 \end{bmatrix} \end{align*}\]

It trivial to observe the mean of each column (each feature) is $0$.

(3.) The covariance is probably:

a. positive are relatively high. It seems that there are correlation between the grade for Math and English; when one is high the other is also high.

b. close to $0$. It seems that there are no tendencies indicating a correlation between grades for English and Art.

(4.) We should use the formulae $C_X = \frac{1}{n}X^TX$. Each row of $X$ correspond to all $m=3$ measurements (a Mathgrade , an English grade, and an Art grade) from one particular trial (a student). Each column corresponds to all $n = 5$ measurements of a particular type (either Math grades, English grades, or Art grades).

Remark: It important that $X$ is mean centered.

(5.) Let’s compute the covariance without Bessel’s correction. Let $M={90,90,60,60,30}$ be the Math grades, $E = {60, 90, 60, 60, 30}$ the English grades, and $A = {90, 30, 60, 90, 30}$ the Art grades. The mean of

  • $M$ is $\bar{m} = 66$
  • $E$ is $\bar{e} = 60$
  • $A$ is $\bar{a} = 60$

cf. (2).

Now we can compute:

  • \[\sigma^2_{MM} = \frac{1}{5}\sum_{i=1}^{5}(m_i-\bar{m})^2 = 504\]
  • \[\sigma^2_{EE} = \frac{1}{5}\sum_{i=1}^{5}(e_i-\bar{e})^2 = 360\]
  • \[\sigma^2_{AA} = \frac{1}{5}\sum_{i=1}^{5}(a_i-\bar{a})^2 = 720\]
  • \[\sigma^2_{ME} = \frac{1}{5}\sum_{i=1}^{5}(m_i-\bar{m})(e_i-\bar{e}) = 360\]
  • \[\sigma^2_{MA} = \frac{1}{5}\sum_{i=1}^{5}(m_i-\bar{m})(a_i-\bar{a})= 180\]
  • \[\sigma^2_{EA} = \frac{1}{5}\sum_{i=1}^{5}(e_i-\bar{e})(a_i-\bar{a}) = 0\]

It is easier to use the formulae from point 4. Let’s do that next. Here we also use Bessel’s correction.

(6.) We have that

a. the covariance matrix without Bessel’s correction is

\[\begin{align*} C_X = \frac{1}{5}X^TX = \begin{bmatrix} 504 & 360 & 180 \\ 360 & 360 & 0 \\ 180 & 0 & 720 \end{bmatrix} \end{align*}\]

b. the covariance matrix with Bessel’s correction is

\[\begin{align*} C_X = \frac{1}{5-1}X^TX = \begin{bmatrix} 630 & 450 & 225 \\ 450 & 450 & 0 \\ 225 & 0 & 900 \end{bmatrix} \end{align*}\]

For $X$ we use the mean centered matrix from point 2.

Task 6 - Projection onto new feature space

When analysing the Iris dataset, we stored the data in form of a $150 \times 4$ matrix where the columns are the different features, and every row represents a separate flower sample. Let’s call this matrix $X$ and the first and the second principal component $w_1$ and $w_2$.

  1. Using matrix multiplication, how do we project the 4-dimensional feature space onto a new 2-dimensional feature space that is spanned by $w_1$ and $w_2$? How does this relate to the formula on page 7 of the slide set?

  2. Give the sizes of the matrices that you used in 1.)

Solution:

(1.) We construct a transformation matrix $W$ of the form

\[\begin{align*} W = [w_1 \ | \ w_2] \end{align*}\]

Afterwards, we make the projection onto the new feature space by computing $Y = X\cdot W$.

This is not quite the formulae from the slides but it’s close. By transposing each side we get

\[\begin{align*} Y = X\cdot W \Leftrightarrow Y^T = W^T\cdot X^T \end{align*}\]

The matrix $W^T$ corresponds to the matrix $P$ from the slides as the row vectors of $P$ should be the newbasis vectors for expressing the columns of $X^T$. The new feature space’s basis vectors are the vectors $w_1$ and$w_2$. These are the column vectors of $W$; thus, they are the row vectors of $W^T$. The matrix $X^T$ has features asrows and samples as columns (since $X$ had samples as rows and different features as columns). The matrix $Y^T$ is thenew representation of the data with principle components as rows (in a sense “new features”) and samples as columns.

(2.) The size of $W$ is $4\times 2$. The size of $X$ is $150\times 4$. Since $Y$ is computed as $X\cdot W$ its size becomes$150\times 2$ (in a sense we have the same samples but now the features have changed to the principle components).

Task 7 - Eigenfaces

In your git repository, beside the files needed for the assignment (helper.py and main.py) you find also the application EigenFace.py.

  1. Run the script and download the images as described.

  2. Run again the script. If all run smoothly you should be able to see the average images and a window with trackbars to change the weights of the principal components. Experiment with different values and observe the changes at the picture. Which characteristic of the image does each principl component captures?

  3. After you have a working solution for the assignment you can uncommnet lines 141-149 and run the script again. Hovering on the window with the picture and pressing a key it is possible to iterate through the images and assess the distance of their PCA projection from the original image. Which face has the largest distance from its PC projection?

Task 8 - Eigenfaces

In your last mandatory assignment you will be using the PCA functionality from OpenCV (https://opencv.org/). For this exercise, we will use another set of tools, namely Google’s Colabatory framework https://colab.research.google.com and, scikit-learn (https://scikit-learn.org), a free software machine learning library for Python for data analytics, statistics, machine learning, and Scipy (https://www.scipy.org/, the scientific Python ecosystem). All of those in itself can be quite overwhelming, however, the idea of this exercise is to experience how easy it is to use and integrate all those.

Proceed as follows:

  1. Download the Jupyter notebook plot_eigenfaces.ipynb from here: https://scipy-lectures.org/packages/scikit-learn/auto_examples/plot_eigenfaces.html (at the very end of the page).

  2. Upload the notebook to https://colab.research.google.com.

  3. Run the cells subsequently (you can safely ignore everything related to Support Vector classification, and anything after “Doing the Learning: Support Vector Machines”).

  4. Add a cell (after cell 8) and print the vector in the 150-dimensional Eigenface-space that corresponds to the projection of the first image in the test dataset X_test.

Solution:

Add this after cell 8:

# First image of test dataset X_test. Note: A row of X_test is an image.
v = X_test[0]
		
# Project first image of X_test onto eigenface-space (space spanned by the 150 principle components).
v_proj = pca.transform([v])
print(v_proj)